NumPy 泊松分布

泊松分布（Poisson Distribution）

泊松分布是一种离散分布。

它估计在指定时间内事件可能发生的次数。例如，如果某人一天吃两次，那么他吃三次的概率是多少？

它有两个参数：

  • lam - 发生率或已知次数，例如 2 对于上述问题。
  • size - 返回数组的形状。

实例

为发生次数 2 生成一个随机的 1x10 分布：

from numpy import random

x = random.poisson(lam=2, size=10)

print(x)

亲自试一试

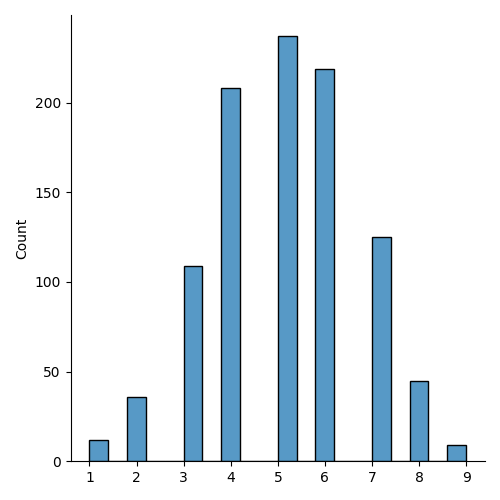
泊松分布的可视化

实例

from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

sns.displot(random.poisson(lam=2, size=1000))

plt.show()

亲自试一试

结果

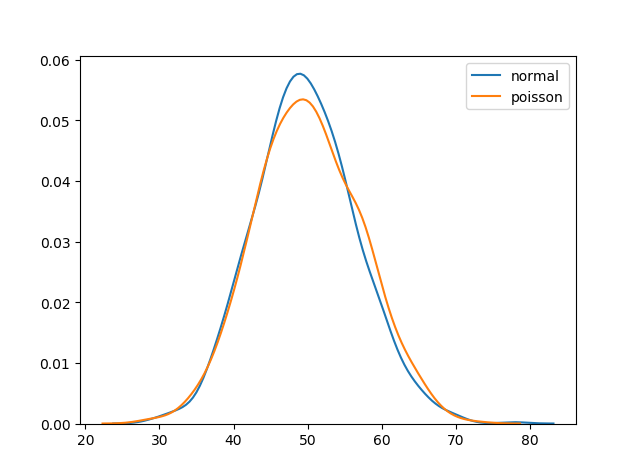
正态分布与泊松分布的区别

正态分布是连续的，而泊松分布是离散的。

但我们可以看到，类似于二项式，对于足够大的泊松分布，它将变得类似于具有特定标准差和均值的正态分布。

实例

from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

data = {
  "normal": random.normal(loc=50, scale=7, size=1000),
  "poisson": random.poisson(lam=50, size=1000)
}

sns.displot(data, kind="kde")

plt.show()

亲自试一试

结果

二项分布和泊松分布之间的区别

二项式分布只有两种可能的结果，而泊松分布可以有无限种可能的结果。

但对于非常大的 n 和接近于零的 p，二项式分布几乎与泊松分布相同，因此 n * p 几乎等于 lam。

实例

from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

data = {
  "binomial": random.binomial(n=1000, p=0.01, size=1000),
  "poisson": random.poisson(lam=10, size=1000)
}

sns.displot(data, kind="kde")

plt.show()

亲自试一试

结果